Logical Sudoku Solver
-
A powerful algorithmic tool designed to conquer even the most challenging Sudoku puzzles without resorting to brute force, guessing, or backtracking. This solver showcases a refined approach to puzzle solving, providing users with detailed insights at every step.
X-Wing example
Techniques
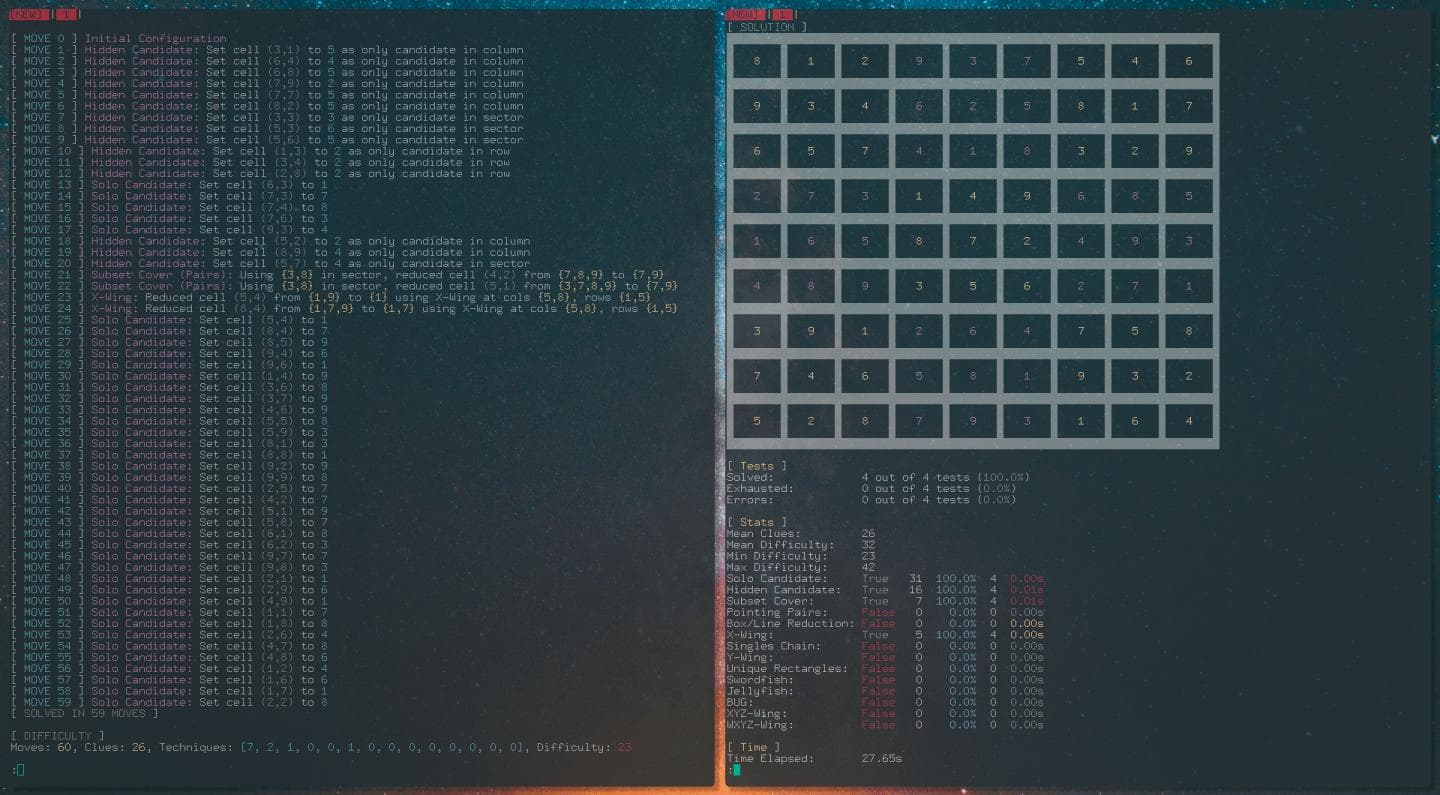
Solo Candidate
The solo candidate technique is a simple technique for identifying the value of cells where a cell has only one candidate, therefore the cell must be that candidate. This technique has been implemented using a O(N2) complexity algorithm as every cell in the grid must be checked. Multiple solo candidates can be observed in one pass of the algorithm. Using only this strategy is not sufficient enough to solve any 17-clue Sudoku.
Hidden Candidate
The hidden candidate technique is another simple technique for identifying the value of cells. If a candidate is valid in only one cell within a column, row or sector then that cell must be that value. This technique has been implemented using a O(N3) complexity algorithm as each cell in a structure (column, row, sector) must be checked against each candidate. Using only the Single Candidate and Hidden Candidate techniques, 44.6% of the 49,151 17-clue Sudoku were solved. However, these two strategies are sufficient enough to solve every simple Sudoku.
Subset Cover (Pairs/Triples/Quads/Quints)
The subset cover technique eliminates candidates within a column, row or sector. If a subset of N cells within a structure covers N different candidates (i.e. union of candidates in the N cells is of size N) then the candidates must be contained within these N cells and cannot appear elsewhere in the structure. This technique is only valid for 2<=N<=5 as any subset of size N greater than 5 will automatically be composed of a smaller subset of size (9-N) which will be simpler to solve.
Pointing Pairs/Triples
The pointing pairs/triples technique eliminates candidates within a column or row. If a candidate occurs either two or three times within a sector and these cells are all within the same column/row, then the value must be located within the sector and cannot occur elsewhere the column/row. This technique has been implemented using a O(N3) complexity algorithm as each cell in every sector must be checked for each candidate.
Box/Line intersection
The box/line intersection technique eliminates candidates within a sector. If a candidate value in a column/row only appears within one sector, then that candidate must occur in the sector in that column/row, and so the candidate can be eliminated from the other cells in the same sector. This technique has been implemented using a O(N3) complexity algorithm as each cell in a column/row must be checked for every column/row.
X-Wing
The X-Wing technique is a subset of single value chaining strategies where a candidate is restricted in two cells along a column in two different columns that all share the same rows. The technique can also be expressed as two conjugate pairs joined by two weak links where the four cells form a rectangle. This technique has been implemented using a O(N3) complexity algorithm.
Singles Chain
The singles chain technique firstly identifies for a given candidate all the conjugate pairs. Then constructs a connected graph of conjugate pairs with nodes of alternating state (ON/OFF). The conjugate pairs are used to find either violations of cells in the graph (two cells of the same state that are in the same structure) or cells not in the graph that can see nodes of both states. This technique has been implemented using an adjacency list to store the graph on conjugate pairs leading to an algorithmic complexity of O(N3).
Y-Wing
The Y-Wing technique is a bi-value chaining strategy that uses three bi-value cells to eliminate candidates. The head of the Y-Wing has candidates AB, there are two wings that share the same structure as the head with candidates AC and BC respectively. Whatever the actual value of the head, either wing must be C. Therefore any cells that intersect with both wings can remove C as a candidate. This technique has been implemented using a O(N3) complexity algorithm.
Unique Rectangles
The Unique Rectangle technique eliminates candidates by preventing a state where there exist multiple solutions. A Unique Rectangle is a group of four cells that form a rectangle of which the cells occupy exactly two sectors. Additionally, three of the cells in the rectangle must be AB and the remaining cell must contain at least AB. This cell cannot be A or B as it would form a rectangle where the A or B are interchangeable.
Swordfish
The Swordfish technique is an extension of the X-Wing technique but where a candidate is restricted in three cells along a column in three different columns that all share the same rows.
Jellyfish
The Jellyfish technique is an extension of both the X-Wing and Swordfish techniques, but with a candidate restricted in four cells along a column in four different columns that all share the same rows.
Bi-Value Universal Grave
The Bi-Value Universal Grave (BUG) is a state that a Sudoku can reach where all unsolved cells in the Sudoku have only 2 candidates, except a single cell that has 3 candidates. The aim of this technique to detect the BUG state and use it to eliminate candidates. This technique has been implemented using a O(N2) complexity algorithm.
XYZ-Wing
The XYZ-Wing technique is an extension of the Y-Wing technique but with the head containing 3 candidates instead of 2. The head of the XYZ-Wing has candidates XYZ, there are two wings that share the same structure as the head with candidates XZ and YZ respectively. Any cells that intersect with all 3 cells of the XYZ-Wing cannot contain the candidate Z. This technique has been implemented using a O(N3) complexity algorithm.
WXYZ-Wing
The WXYZ-Wing technique is a further extension of Y-Wing and XYZ-Wing but with the head containing 4 candidates and three wings that share candidates with the head and have a single common candidate between all 4 cells. If all cells in the WXYZ-Wing have candidate Z, then candidate Z can be removed from every cell that intersects with all 4 cells of the WXYZ-Wing.
Screenshots

